According to the Second Law of Thermodynamics we live in a universe that irreversibly decays over time. But if this is indeed the case, then it begs the question: “How does Evolution’s Spontaneous and Progressive Complexity occur without some form of External Organizing Force?”
Evolution vs. Entropy
The Second Law of Thermodynamics (SLOT) is a law of physics that deals with “Spontaneous Change” (i.e. change that occurs without any external direction, change that happens all by itself…)
The SLOT is, more precisely, the law of physics that deals with how energy distributes itself within a thermal system, always moving spontaneously and irreversibly to “Thermal Equilibrium”.
In everyday terms the SLOT is simply the fact that hot coffee and cold milk, if left unstirred, will spontaneously mix themselves (in both composition and temperature), and will never spontaneously un-mix.
Despite the fact that this seems rather obvious and trivial behavior, the SLOT is nonetheless considered to be one of the most fundamental and important laws of physics — and the reason for this exalted status is that the SLOT is both a “Probabilistic Law” and also the “Law of Maximum Entropy”!
“Entropy” is a concept that deals with amount of “disorder” in a system, and it is widely understood that the spontaneous gravitational pull to maximum entropy is not restricted to simple thermal systems; but that all systems, if left undisturbed, will spontaneously gravitate towards a state of maximum disorder — a state that would seem to be the exact opposite of Nature’s “spontaneously self-organized complexity”.
This apparent conflict between physics and natural evolution obviously begs the question: “How does Evolution manage to spontaneously generate such incredible Complexity in the face of the SLOT?”
How can natural complexity spontaneously arise in a universe dominated by the SLOT and its spontaneous and irreversible pull to disorder? What exactly is the “Source” of all of Nature’s spontaneous order and complexity?
The Export of Entropy
In 1977, the Belgian chemist Ilya Prigogine won the Nobel Prize for Chemistry, for his work on his “Theory of Dissipative Structures”. Prigogine’s theory suggests that complex ordered systems can indeed come into existence if these systems are open and capable of “exporting” their internal disorder, to the external environment.
But while this theory would seem to go some way towards solving the paradox of how order can occur without negating the SLOT, it still does not manage to identify what fundamental forces are actually driving evolution to evermore progressive complexity. Physics has as yet offered no explanation for “evolution’s progressive arrow of time”…
As it turns out however, the resolution of this paradox is actually quite easy. To resolve this apparent conflict between physics and natural evolution we need merely to focus on a very simple fact that has been consistently overlooked about the “probabilistic” SLOT; the fact that it relies heavily on the “Law of Large Numbers (LLN)”…
The LLN
Most people are familiar with the concept that if we toss a coin four times, we won’t necessarily get a 50/50 split of heads and tails: indeed, we could actually get 4 tails in a row. But if we toss the same coin a million times, we will almost certainly get something close to a 50/50 split. It is the LLN that ensures that one million coins tosses will produce an average of 50% heads and 50% tails.
[Note: In the simplest possible mathematical terms, the reason the LLN works so well is that the number of independent tosses (i.e. 1,000,000) is significantly larger than the number of options available to each toss (i.e. 2 – heads or tails).]
The SLOT states that left undisturbed all systems gravitate towards the “most probable state”, a state that is referred to as “thermal equilibrium”. In reality however, the achievement (and sustainment) of thermal equilibrium relies heavily on the number of independent elements (of the system) being significantly larger than the number of energy options available to each element. Which means that the chances of any “statistical deviations” from the “most probable state” are extremely small, and consequently the system as a whole will (virtually) always exhibit uniformity.
So although on the “microscopic level” (of particle interaction) there is a lot of energetic dynamics and non-equilibrium abnormalities, these dynamics and abnormalities are normally invisible on the macro “system level” thanks to both the “Damping” and “Balancing Effects” of the LLN…
The RLLN
Our universe is fundamentally a universe of “systems”, and the probabilistic pull of equilibrium is a concept that is applicable to all fluid and fluid-like systems.
Now, in a thermal system there are billions of tiny particles which interact through collisions, but other than that we can more or less say that they behave completely independently of each other.
Systems however, where the parts – be they particles, elements, components, entities, agents, organizations, etc – behave independently of each other are actually quite rare. Many systems are populated by adaptive elements or agents, and the behavior of these agents has a tendency to weaken the gravitational pull of equilibrium by engineering the “Reverse Law of Large Numbers (RLLN)”…
[Note: Since the LLN relies on the number of independent elements being significantly larger than the number of options available to each element, there are therefore two things can engineer the RLLN and they are: either the number of independent elements in the system comes down, or, the number of options available to each element goes up…]
RLLN 1: Emergent Positive Feedback
In all fluid-like systems, the LLN ensures the spontaneous movement to a “global equilibrium”; however for very small regions within these systems, there are not enough particles to ensure a “local equilibrium”. At the very lowest level within all systems, random fluctuations are undampable and occurring all the time which means that local imbalances are constantly, and randomly, flittering in and out of existence.
Occasionally these random temporary fluctuations can randomly be very persistent. In a thermal system this is naught but a mere statistical curiosity, but in a complex adaptive systems it can easily happen that some parts within the system will begin to adapt to these persistent fluctuations; and often such adaptation can serve to amplify the imbalance even further, and in so doing, further extend the fluctuation’s duration. Thus random local fluctuations can lead to the localized emergence of positive feedback which reduces the independence of the elements and ultimately has an unbalancing and reversing effect on the LLN.
RLLN 2: Insufficient Negative Feedback
Positive Feedback however is not the only thing that can engineer the RLLN. Since the LLN effectively operates like a negative feedback system (in that it dampens a system to a equilibrium) it should be no surprise that the movement away from equilibrium could also be the result of insufficient negative feedback.
So although complex fluid-like systems might gravitate towards equilibrium, many can hold themselves some distance away from equilibrium by exhibiting excessive undampable adaptation and innovation. Adaptation and innovation effectively increases element “Optionality” and such increased optionality among the elements of the system can also engineer the RLLN…
Self-Integration For Free
So the reality of probability driven dynamics in the natural world is that just as the LLN pulls a system to thermal equilibrium, so too the RLLN can hold, or drive, a system away from equilibrium.
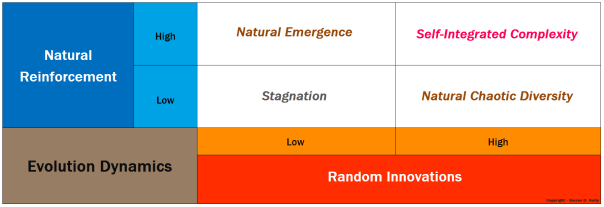
But ultimately what is most interesting about all of this probabilistic behavior is that: while strong positive feedback in isolation can cause the emergence of self-reinforcing local segregation; and while insufficient negative feedback in isolation can cause the surfacing of incompressible innovative diversity; the most interesting stuff actually occurs at the intersection between the two…
Positive reinforcement in a system of great diversity can spontaneously produce surprisingly complex “Integrated Diversity”. So in other words,
with the co-emergence of diversity
Complex-Integration comes for Free!..
Natural Complexity
Evolution’s progressive complexity is often portrayed as spontaneous “Self-Organization”, but this is not the exactly accurate. The secret sauce of evolution’s spontaneous and progressive complexity is actually spontaneous “Self-Integration”.
In the simplest possible terms, Natural Complexity emerges from the finely-tuned self-integration of co-emergent self-organized diversity; and as a consequence “the complex whole is forever becoming greater that its less complex parts”…
So there we go, Natural Complexity explained (by mathematical probability). “Easy Peasy Lemon Squeezy”…
In a universe supposedly dominated by the SLOT what drives nature’s progressive evolution is simply the mathematical interplay of the two distinct forms of the Reverse Law of Large Numbers…
What drives evolution’s spontaneous and progressive complexity is the interplay of insufficient negative feedback and strong positive feedback; or in other words what drives evolution is The Interplay of Random Innovation and Natural Reinforcement…